How to Know Which Master Theorem to Use

By Da_Angelina151 25 Apr, 2022 Post a Comment

We have a9 b3 ânn for this recurrence and consequently n log b a n log 3 9 θn 2. A trick that might work is finding a substitution that transforms the recurrence in.

Master Theorem In Data Structure Dot Net Tutorials

It is pretty simple to eliminate the inhomogeneous part by setting T n A n k n for a suitable constant k.

. The master method has 3 rules. Ө n logba if -- f n є O n logba-ε O n logba-ε O n log24-ε O n2-ε nlog n O n log24-ε -- works. Now fn Θ1 Θnlog b a Θn0 Θ1.

As we already saw the run-time of an algorithm must be expressed as follows to apply the master theorem. If a 1 and b 1 are constants and fn is an asymptotically positive function then the time complexity of a recursive relation is. Where n size of the problem a number of sub-problems b size of each sub-problem.

To apply the master method we simply decide which case of the master theorem applies if any and record the result. There are 3 cases. Tn aTnb Өn klog p n a 1 b 1 k 0 and p R.

If fn On log b a-ϵ then Tn Θn log b a. B 1 k 0 and p is a real number. D loga base b Time Complexity On loga base b Case 2.

A recurrence relation is a type of equation where each. Assumesall subproblems are of equal size most algorithms do this The same amount of data is given to each recursive call An algorithm that splits the subproblems into 13 and 23 or an algorithm that splits data randomly must be solvedin a different manner. Where n size of the problem.

Using Θ notation will be more appropriate fo the master theorem. A should be greater than or equal to 1. The Master Theorem is a recurrence relation solver that is a very helpful tool to use when evaluating the performance of recursive algorithms.

We write the given recurrence relation as T n 3T n3 n. N Θ n 3 hence T n Θ n 3. What does it solve.

Black Box for solving recurrences. It is possible to determine the asymptotic form of T T T based on a relative comparison between f f f and n log b a nlog_ba n lo g b a. The least relation implies A n Θ 8 log 2.

Given a recurrence of the form. Now we can easily apply Masters theorem. Using the second form of Master Theorem Tn Θn0 logn Θlogn.

Ba n1. What Is The Master Theorem. The key to memorizing the master theorem is to simplify it.

We compare the given recurrence relation with T n aT nb θ n k log p n. Theres an approximation to reality that is correct in 99 of the cases. There are some limitations of this theorem.

E Tn 4Tn2n2 logn. Using The Master Theorem we can easily deduce the Big-O complexity of divide-and-conquer algorithms. D loga base b Time Complexity On d logn Case 3.

Master theorem is used to determine the Big O upper bound on functions which possess recurrence ie which can be broken into sub problems. T n a T n b f n Tn a Tleftfrac nbright fn T n a T b n f n. The term f n n log.

If f n is O n k then. Let T n be a function defined on positive n as shown below. But we can come up with an upper and lower bound based on Master Theorem.

Master Theorem for Solving Recurrences. We can use either Theta Θ Notation or Omega Ω Notation instead of Big O Notation. Tn aTnb fn where Tn has the following asymptotic bounds.

This does not form any of the three cases of Master Theorem straight away. A number of subproblems in the recursion and a 1. Nb size of each subproblem.

Now Masters Method determines the Asymptotic Tight Bound Θ or Theta on these recurrences considering 3 Cases. This arises in the rst case of the Master Theorem because if bathen log. Tn aTnbfn where a 1 and b 1 are constants and fn is an asymptotically positive function.

Show activity on this post. A n 8 A n 2 by picking k 160 3. Consider the following scenario.

N is not in any of the three forms required by the three cases of the theorem. Now let us consider three cases. This is because in the general form we have θ for function f n which hides constants in it.

On the other hand if bathen we have an overall decrease in time for example if Tn 2Tn3 then the subproblems are 13 the size and there are only two thats good better than n. Master Theorem For Subtract and Conquer Recurrences. A CASE 2 - if f n Θnlogba f n Θ n log b.

Now a 3 and b k 3 1 3. A good but not technically correct summary of the Master Theorem is as follows. Practice Problems and Solutions Master Theorem The Master Theorem applies to recurrences of the following form.

This theorem is an advance version of master theorem that can be used to determine running time of divide and conquer algorithms if the recurrence is of the following form -. If fn Θn log b a then Tn Θn log b a log n. D loga base b Time Complexity On d Proof Of Master Theorem.

How to use Master Theorem Analysis of Algorithms. Using Mas-ter Theorem a 1b 2fn Θ1. Look at the first case if the runtime of f n is smaller than n2.

A ϵ for some ϵ 0 ϵ 0 then T n Θnlogba T n Θ n log b. If a 1 and b 1 are constants and fn is an asymptotically positive function then the time complexity of a recursive relation is given by. The Masters Theorem states.

This means that the problem is at least reduced to a smaller sub problem once. If a b k then Tn Θ n log b a log b a log a log b. If fn Onlogb a for some constant 0 then Tn Θnlogb a.

It solves recurrences of the form Tn aTnb fn. As it is you cant use Master Theorem for this recurrence. Tn 2 Tn2 On Recurrence Equation.

As ân0n log 3 9-ϵ where ϵ1 we can use case 1 of the master theorem to determine that Tnθn 2. For some constants c a0 b0 k0 and function f n. Ba.

F n has O n2-ε as upper limit for worst case. If fn Onlog_b a - epsilon then Tn Theta nlog_b a If fn Theta nlog_b a then Tn Theta nlog_b a logn If fn Omega nlog_b a epsilon then Tn Theta fn We will use some examples to show how the master theorem works. There are 3 cases for the master theorem.

Recurrences occur in a divide and conquer strategy of solving complex problems. If TnaTnb fn then compare nlog_b a with fn If fn nlog_b a then Tnnlog_b a. If fn Θnlogb a logk n with1logb a logk.

Suppose we are given a Recurrence Relation Tn 16 Tn4 n. Let us understand this Case with example. The master theorem is used in calculating the time complexity of recurrence relations divide and conquer algorithms in a simple and quick way.

A then T n Θnlogbalgn T n Θ n log b. A n k n 8 A n 2 4 k n 160 n. CASE 1 - if f n Onlogbaϵ f n O n log b.

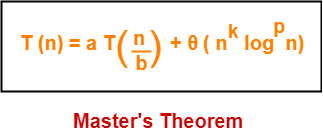
Master Theorem Master Theorem Examples Gate Vidyalay